design_fir_freq
Frequency sampling design.
Namespace: dsp::filter
Prototype
Vecf design_fir_freq(int n, const Vecf &d)
Parameters
| n | Filter order (must be odd). |
| d | Vector with desired frequency response (positives frequencies). |
Returns
Vector with FIR filter coefficients (dimension = \(n\)).
Description
This method enables to approximate with a FIR filter with \(n\) coefficients ( \(n\) being odd) an arbitrary frequency response, given as a specification. The frequency specification must be given as a vector \(d\) of \(m=\frac{n+1}{2}\) real elements, of type:
The frequencies \(f_k\) can be computed with the function design_fir_freq_freqs().
- Note
- Note that the elements \(m\) of the frequency response enable to specify uniquely a real filter with \(n=2m-1\) coefficients (indeed, each element of the response, except for the first, is used twice, for positive and negative frequencies). Thus, if \(n\neq 2m-1\), the desired frequency response is, before computing the filter coefficients, resampled (by linear interpolation) with \(m'\) values such as \(n=2m'-1\) (in every case, the number of coefficients must be odd).
Example
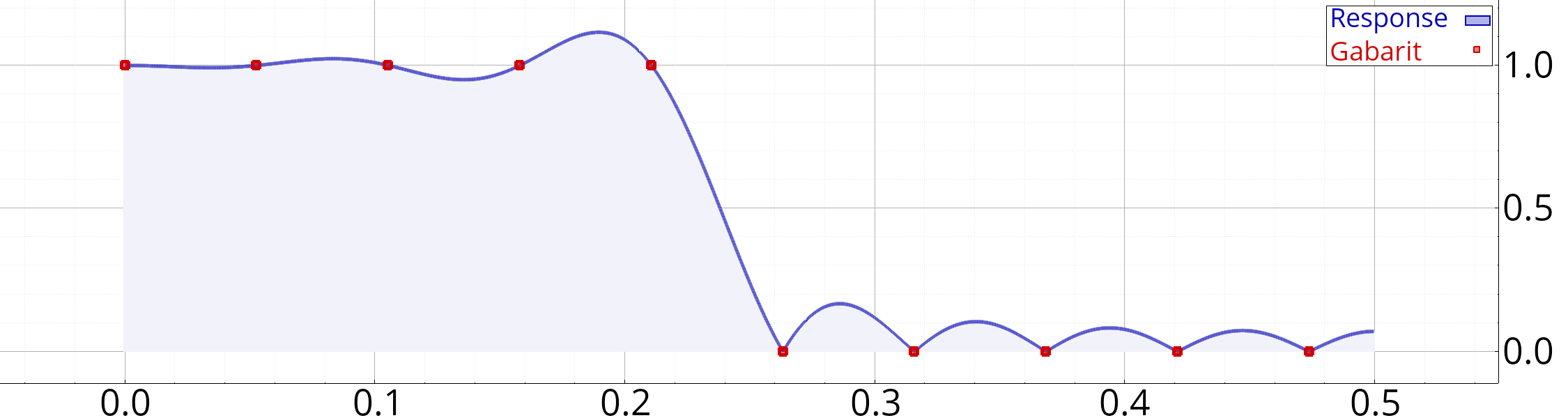
// Nombre de coefficients souhaités soit n = 19;
// Nombre de points du gabarit soit m = (n + 1) / 2; // m = 10 // Réponse désirée (ici simple filtre passe-bas) // (il est possible de changer ce vecteur de manière arbitraire) soit d = Vecf::zeros(m);
d.head(m/2).setConstant(1);
// Calcul des coefficients du filtre soit h = design_rif_freq(n, d);
// Plots Figure f;
// Réponse réelle soit [fr,xm] = frmag<float>(h);
soit c = f.plot(fr, xm, "b-" , est_fr() ? "Réponse" : "Response" );
c.def_remplissage(oui, oui, 0);
// Gabarit soit fr1 = design_rif_freq_freqs(n);
c = f.plot(fr1, d, "rs" , "Gabarit" );
Frequency response
