design_iira

IIR design from a classical analog prototype.

Namespace: dsp::filter

Prototype

FRat<cfloat> design_iira(int n, cstring type, cstring prototype, float fc, float δ_bp=0.1f, float δ_bc=60)

Parameters

n	Fitler order.
type	Filter type ("lp" for low-pass, "hp" for high-pass, ...)
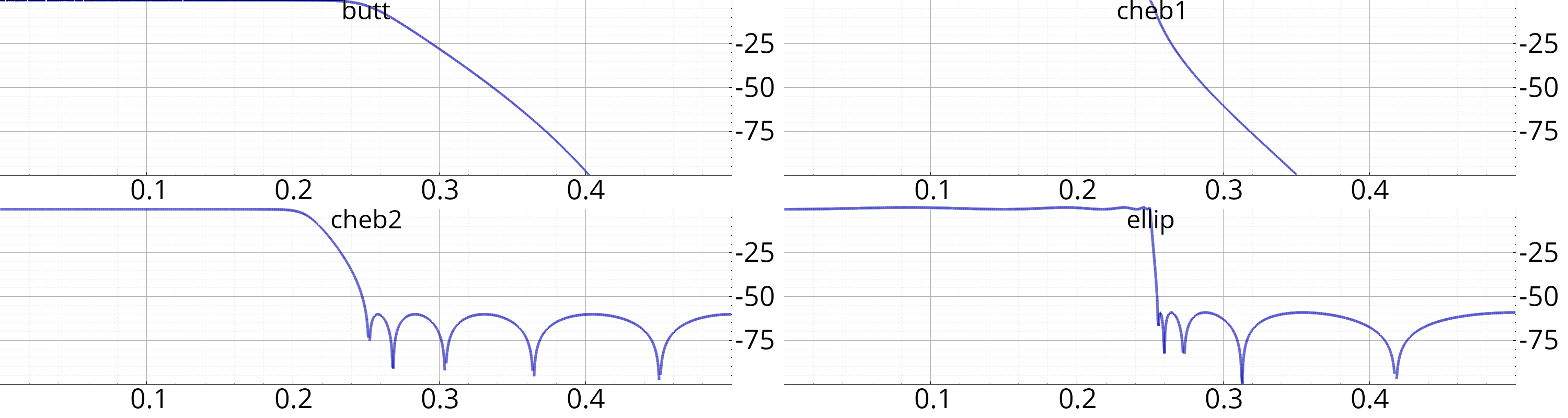
prototype	"butt", "cheb1", "cheb2" or "ellip"
fc	Normalized cut-off frequncy (or central frequency for band-pass and band-stop), between 0 and 0.5.
δ_bp	Maximal ondulation (in decibels) in the pass-band (used only for Chebychev type I or elliptic filters).
δ_bc	Minimal attenuation (in decibels) in the sto-band (used only for Chebychev type II or elliptic filters).

Returns

h Transfert function (digital)

Description

This function returns a discrete transfert function, in the form of poles and zeros (ideal for an implementation with second order sections, see filter_sois()). The following prototypes are possible:

Butterworth (no ondulation, wide transition band)
Chebychev type I (ondulations in the pass-band)
Chebychev type II (ondulations in the stop-band)
Elliptique (ondulations everywhere, but shortest transition band)

The filter is first designed in the analog domain (Laplace transform), then converted in digital form (z transform) with the bilineair transform.

Example


  // Test des 4 types de filtre, avec les paramètres suivants :
  // - Filtres passe-bas (lp = low-pass)
  // - Fréquence de coupure       = fe/4
  // - Ondulation bande passante  = 1 dB  (Chebychev type I & elliptique)
  // - Atténuation bande coupée   = 60 dB (Chebychev type II & elliptique)
  Figures f;
  for(auto type: {"butt", "cheb1", "cheb2", "ellip"})
  {
    soit h = design_riia(10, "lp", type, 0.25, 1, 60);
    soit [fr, xm] = frmag(h);

    f.subplot().plot(fr, mag2db(xm), "b-", type);
    // pour pouvoir comparer les réponses entre elles
    f.gcf().def_rdi({0, -100, 0.5, 100});
  }