filter_fft

• Documentation
• / Fourier transform
• / filter_fft

Creation of frequency domain filter (OLA / OverLap-and-Add technique).

Namespace: dsp::fourier

Prototype

tuple<sptr<Filter<cfloat, cfloat, FiltreFFTConfig>>, int> filter_fft(const FFTFilterConfig &config)

Parameters

Returns

A tuple with two elements:

• the OLA filter,
• an integer which is the dimension \(N\) of the FFT (that is, the dimension of the vectors that will be given to the callback).

Description

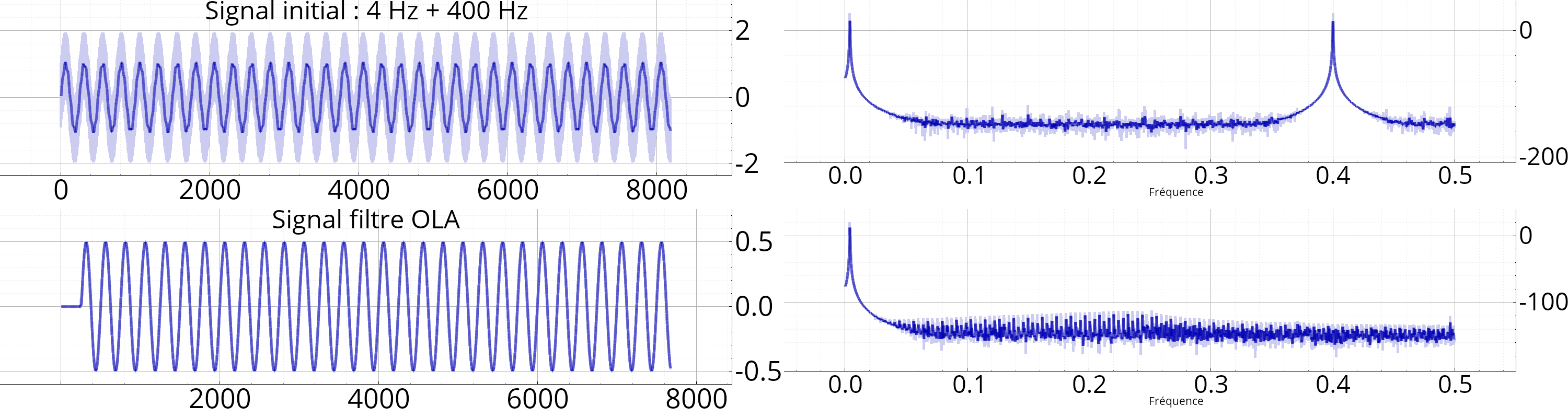
For different purposes, it can be convenient to apply filtering in the frequency domain rather than in the time domain, for instante to reduce the computing load. (time domain convolutions become simple term by term product in the frequency domain). By frequency domain filtering, we mean here to be able to adjust term by term the different bins of the DFT of a signal, and then to build the result in the time domain.

So as to work in the frequency domain, samples are grouped into blocks of \(N_e\) samples, and for each of these blocks the following operations are performed:

• Windowing and overlap (optional): so as to smooth processings from one block to the next one, an apodisation window is applied (by default, a Hann window with an overlap of 50 %, so as to enable perfect reconstruction of the time domain signal).
• Zero-padding : So as to compute efficiently the FFT, zeros are inserted, making the length of each block equal to some power of 2. So, after zero-padding, the blocks length is \(N=2^k\geq N_e\).
• Fourier transform: through a FFT.
• Frequency domain processing : through a callback provided by the caller (see below).
• Inverse Fourier transform.
• Recomposition of time domain blocks: through the OLA technique (OverLap-and-Add).

Note

For the more specific problem of efficient FIR filter computing (using the FFT), use rather filter_fir_fft(), which is based on this function, and is simpler to use.

Example: Low-pass filter

In this example, we low-pass filter a signal by simply zeroing half the spectrum.

  soit n = 8192;
  // signal utile à f = 0.04 * fe Hz, et parasite à f=0.400 * fe Hz
  soit x = (sigsin(0.004, n) + sigsin(0.4, n)).as<cfloat>();


  FiltreFFTConfig config;
  // Cette callback sera appelée à chaque itération de l'OLA
  config.traitement_freq = [&](Veccf &X)
  {
    assertion(X.rows() == 512);
    X.segment(128, 256).setZero();
  };
  config.dim_blocs_temporel   = 512;  // Par bloc de 512 échantillons
  config.nb_zeros_min         = 0;    // Zéro-padding non nécessaire
  config.avec_fenetrage       = oui;  // Fenêtre de Hann et recouvrement de 50 %

  soit [ola, N] = filtre_fft(config);
  soit y = real(ola->step(x));

See also

filter_fir_fft(), filter_rfft(), ola_complexity(), ola_complexity_optimize()