Matrice de Fourier

• Exemples
• / Transformée de Fourier
• / Matrice de Fourier

La TFD ( \(X_j = \sum_i x_i\cdot e^{2\pi\mathbf{i} ij/N}\)) peut s'exprimer de manière matricielle via la matrice de Fourier \(F\) : \[ X = F \cdot x \] Avec : \[ F_{ij} = e^{2\pi\mathbf{i} ij/N} \]

Ici, on affiche la phase de cette matrice (la magnitude étant constante).

Figure plot_mat_fourier(entier N)
{
  Tabf phase(N,N);

  pour(auto i = 0; i < N; i++)
    pour(auto j = 0; j < N; j++)
      phase(i,j) = modulo_2π(-(2*π*i*j)/N);

  Figure f;
  f.axes().set_isoview(oui);
  f.axes().supprime_decorations();
  // Carte de couleur HSV, car périodique
  f.plot_img(phase, "hsv");

  retourne f;
}

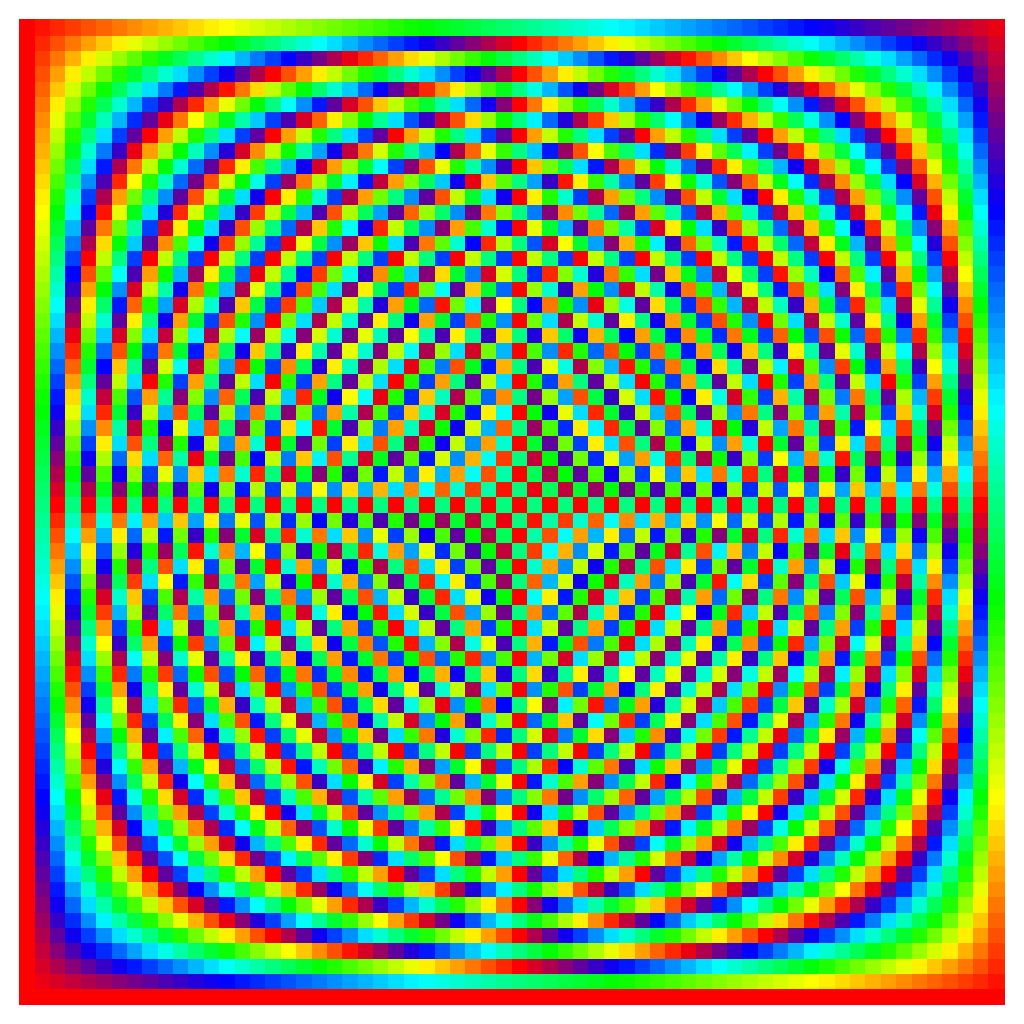
N = 64

Chaque sortie \(X_i\) de la TFD peut être interprétée comme le produit scalaire du signal d'entrée avec la ième ligne de la matrice : \[ X_i = \left<x, F_{i,.}\right> \]

Les termes de basses fréquences (positives) sont en bas (notez la ligne de bas, de phase constante, qui correspond à \(X_0\)). Ensuite, plus on monte, plus la fréquence est élevée, du moins jusq'au milieu, c'est-à-dire pour le terme \(X_{N/2}\), après quoi on passe sur les fréquences négatives).