filter_goertzel

Filtre de Goertzel (calcul au fil de l'eau)

Namespace: dsp::fourier

Prototype

sptr<FilterGen<float>> filter_goertzel(float frequence, int N)

Parameters

frequence	Fréquence à détecter (normalisée à la fréquence d'échantillonnage).
N	Nombre de points de la TFD équivalente (facteur de décimation)

Returns

Filtre générique float -> float

Description

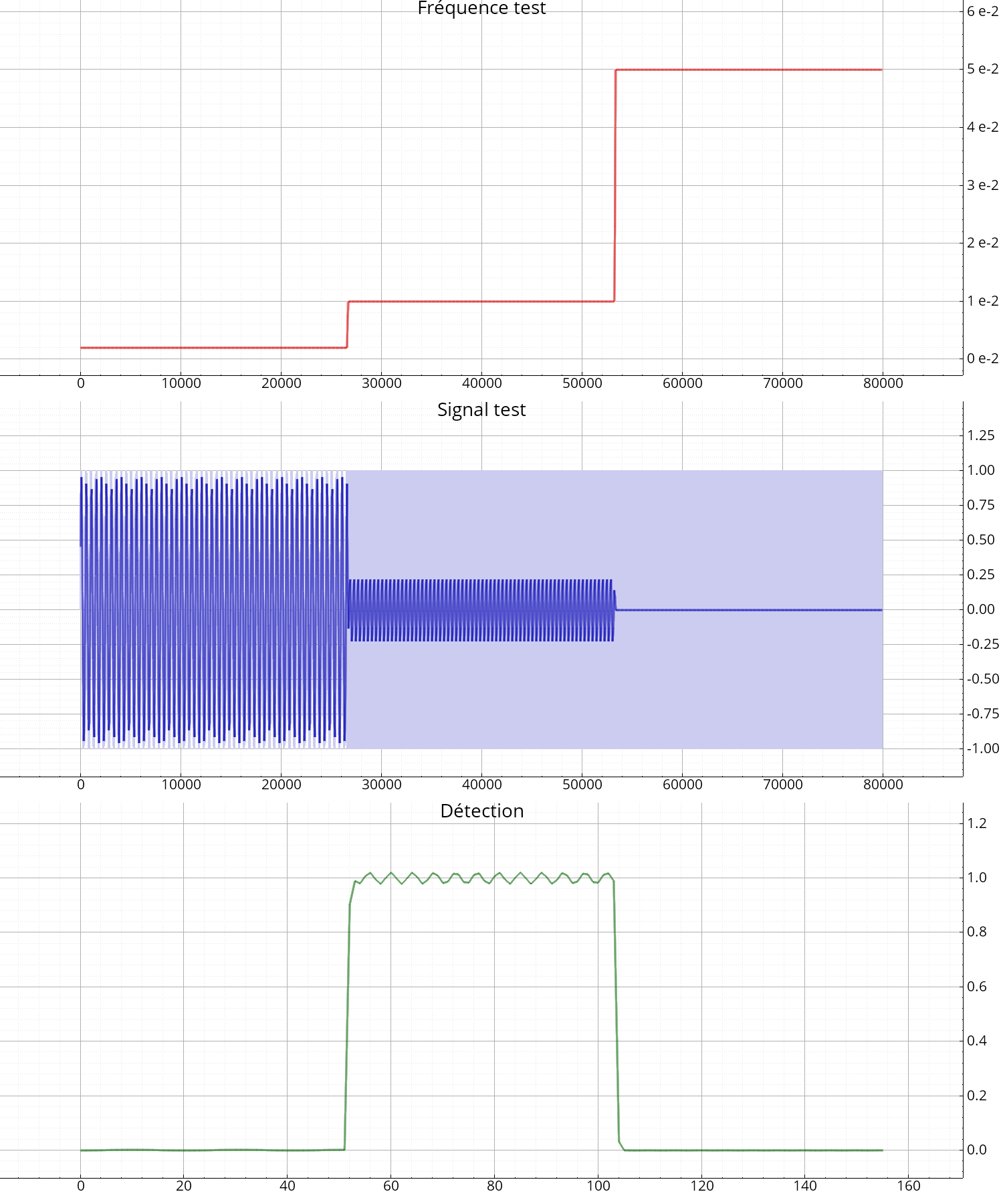
Ce filtre calcule au fil de l'eau la densité de puissance (normalisée à la puissance totale du signal) à une fréquence donnée (voir goertzel()).

Le calcul est fait par blocs de \(N\) échantillons, et la fréquence d'échantillonnage en sortie est donc divisée par \(N\) par rapport à la fréquence d'entrée (1 échantillon produit pour \(N\) échantillons consommés) : \[ y_i = \frac{\left|2\cdot\mathcal{F}(x_{Ni\dots Ni + N-1})(f)\right|^2}{\displaystyle{\sum_{k=Ni}^{Ni+N-1}{x_k^2}}} \]

\(\mathcal{F}(.)\) étant la transformée de Fourier discrète.

Le paramètre \(N\) correspond donc au nombre de points de la transformée de Fourier, et la résolution fréquentielle sera donc d'autant plus fine que \(N\) est grand.

Exemple : détection d'une sinusoïde pure


  // Tableau des fréquences :
  // fréquence cible seulement au milieu
  soit vfreq = freq * Vecf::ones(n);
  vfreq.head(n/3).setConstant(freq * 0.2);
  vfreq.tail(n/3).setConstant(freq * 5.0);


  // Filtre de Goertzel au fil de l'eau
  soit g = filtre_goertzel(freq, N);

  // Signal de fréquence variable
  soit x = sin(2 * π * vfreq * linspace(0, n-1, n)),
       y = g->step(x);

  // Affichages
  Figures f;
  f.subplot().plot(vfreq, "r-", est_fr() ? "Fréquence test" : "Test frequency");
  f.subplot().plot(x, "b-", est_fr() ? "Signal test" : "Test signal");
  f.subplot().plot(y, "g-", est_fr() ? "Détection" : "Detection");