doppler_distri

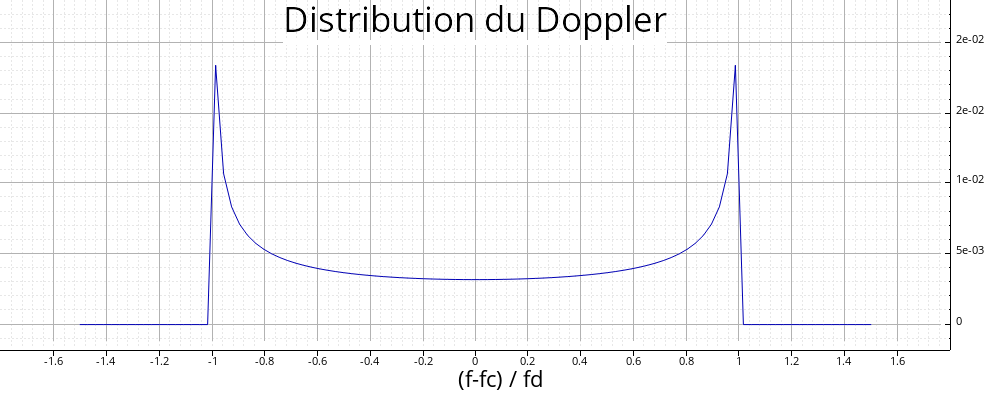
Densité spectrale due au Doppler (modèle statistique).

Namespace: dsp::telecom

Prototype

Vecf doppler_distri(const Vecd &f, float fd, double fc)

Parameters

f	Tableau de fréquence où calculer le spectre
fd	Doppler maximum (d'après la vitesse relative max. du mobile)
fc	Fréquence porteuse

Returns

\(P(f)\) (en densité de probalité / Hz)

Description

Pour un canal avec multiples trajets et un objet mobile, les fréquences reçues pour chaque trajet possible sont décalées suivant le Doppler \(f_d^{max} \cos \theta\), \(\theta\) étant l'angle d'incidence du trajet, et \(f_d^{max}\) le Doppler maximal correspondant à un trajet aligné avec la direction de déplacement du mobile.

Si on suppose toutes les directions incidentes équiprobables, sans qu'il n'existe de trajet dominant (modèle de Rayleigh), alors on peut montrer que le décalage Doppler est dristribué suivant la loi (modèle de JAKES) : \[ P(f) = \frac{1}{\pi f_d \sqrt{1-\left(\frac{f-fc}{fd}\right)^2}} \]

Warning

En passant en paramètre le tableau des fréquences (paramètre f), soyez vigilant qu'en général le doppler est une petite valeur par rapport à la fréquence porteuse. De ce fait, il faut absolument représenter ces fréquences en double précision (comme dans l'exemple ci-dessous).

Example


  soit fc = 900e6f, fd = 100.0f;

  // Tableau de fréquences, relative à la fréquence porteuse (flottant 32 bits ok)
  soit freq_rel = linspace(- 1.5 * fd, 1.5 * fd, 100);

  // Tableau de fréquences, en valeur absolue (nécessité d'utiliser une double précision ici)
  soit freq_abs = freq_rel.as<double>() + fc;

  soit S = doppler_distri(freq_abs, fd, fc);

  Figure f;
  f.plot(freq_rel / fd, S);
  f.titres("Distribution du Doppler", "(f-fc) / fd");