design_rif_freq
Design par échantillonnage fréquentiel.
Espace de nom : tsd::filtrage
Prototype
Vecf design_rif_freq(entier n, const Vecf &d)
Paramètres
| n | Ordre du filtre (doit être impair). |
| d | Vecteur définissant la réponse fréquentielle souhaitée (sur les fréquences positives). |
Retourne
Vecteur des coefficients du filtre (dimension = \(n\)).
Description
Cette technique permet d'approximer avec un filtre RIF de \(n\) coefficients ( \(n\) étant impair) une réponse fréquentielle arbitraire (mais discrète), passée en paramètre. La réponse fréquentielle doit être donnée sous la forme d'un tableau \(d\) de \(m=\frac{n+1}{2}\) éléments réels, de type :
Les \(f_k\) peuvent être obtenus par la fonction design_rif_freq_freqs().
- Note
- Notez que \(m\) éléments de réponse fréquentielle permettent de spécifier de manière unique un filtre réel avec \(n=2m-1\) coefficients (en effet, chaque élement de la réponse fréquentielle, sauf le premier, est utilisé une deuxième fois, pour les fréquences négatives). Par conséquent, si \(n\neq 2m-1\), la réponse fréquentielle souhaitée est, avant calcul du filtre, ré-échantillonnée (par interpolation linéaire) avec \(m'\) valeurs de tel sorte que \(n=2m'-1\) (dans tous les cas, le nombre de coefficients doit être impair).
Exemple
// Nombre de coefficients souhaités soit n = 19;
// Nombre de points du gabarit soit m = (n + 1) / 2; // m = 10 // Réponse désirée (ici simple filtre passe-bas) // (il est possible de changer ce vecteur de manière arbitraire) soit d = Vecf::zeros(m);
d.head(m/2).setConstant(1);
// Calcul des coefficients du filtre soit h = design_rif_freq(n, d);
// Plots Figure f;
// Réponse réelle soit [fr,xm] = frmag(h);
soit c = f.plot(fr, xm, "b-" , est_fr() ? "Réponse" : "Response" );
c.def_remplissage(oui, oui, 0);
// Gabarit soit fr1 = design_rif_freq_freqs(n);
c = f.plot(fr1, d, "rs" , "Gabarit" );
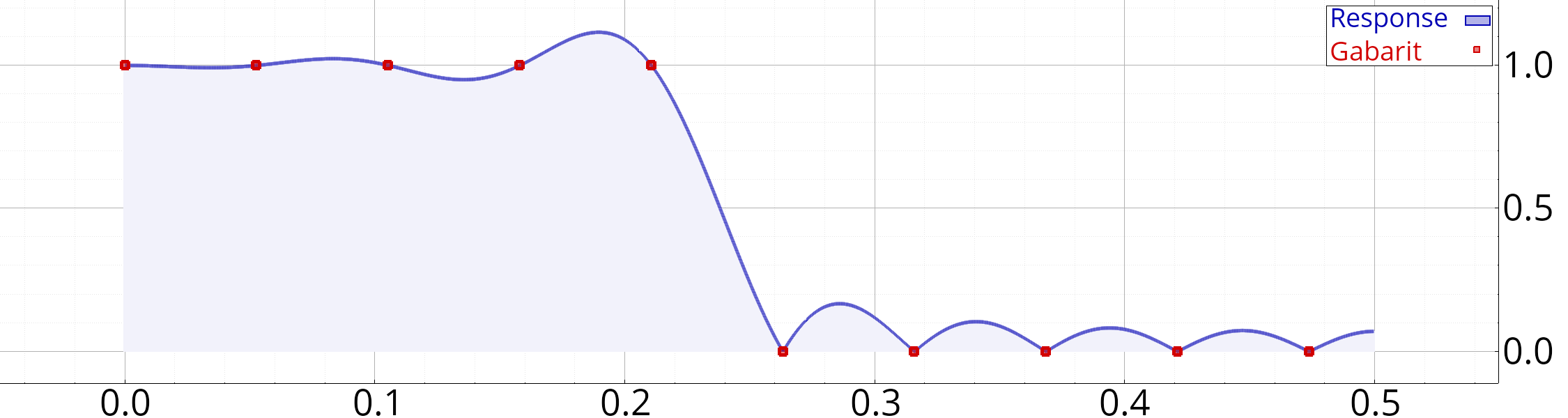
Réponse fréquentielle
