filtre_fft

Création d'un filtre dans le domaine fréquentiel (technique OLA / OverLap-and-Add).

Espace de nom : tsd::fourier

Prototype

tuple<sptr<Filtre<cfloat, cfloat, FiltreFFTConfig>>, entier> filtre_fft(const FiltreFFTConfig &config)

Paramètres

configLa structure de configuration (FiltreFFTConfig) doit préciser la dimension \(N_e\) des blocs temporels, le nombre minimum de zéros à insérer avant chaque bloc et avant de passer dans le domaine fréquentiel, ainsi qu'une callback permettant à l'appelant de modifier le signal dans le domaine fréquentiel.

Retourne

Un tuple de deux éléments :

  • le filtre OLA,
  • un entier indiquant la dimension \(N\) des FFT (c'est-à-dire la dimension des vecteurs qui seront passés à la callback)

Description

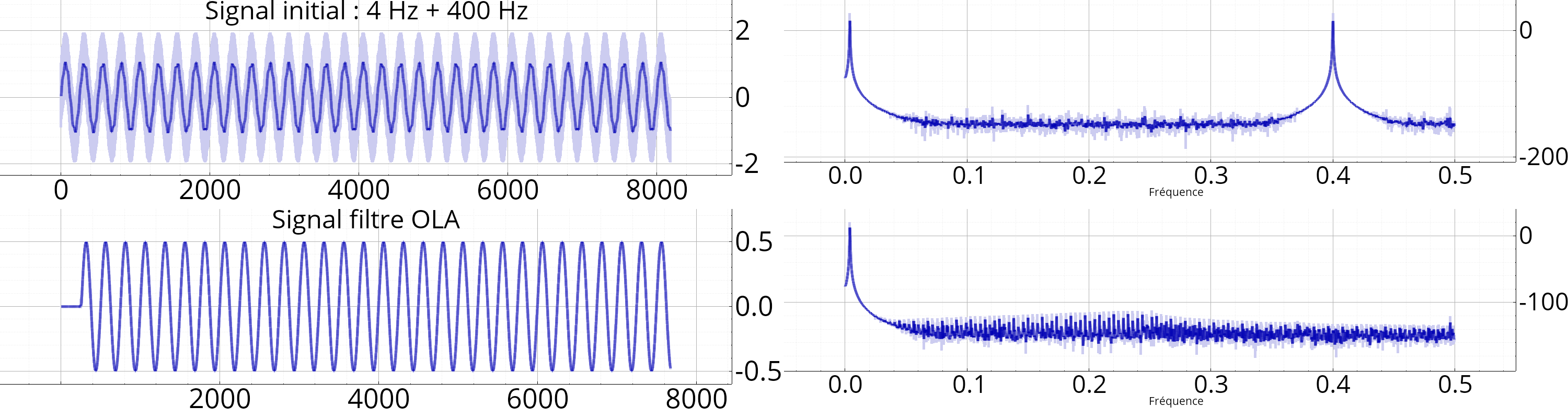
Pour différentes raisons, il peut être plus intéressant de filtrer dans le domaine fréquentiel que temporel, par exemple pour alléger la charge de calcul (les convolutions dans le domaine temporel deviennent de simples produits termes à termes en fréquentiel). Par filtrage fréquentiel, on entends le fait de pouvoir modifier terme par terme les composantes de la transformée de Fourier d'un signal, puis de pouvoir restituer un signal temporel.

Afin de travailler dans le domaine fréquentiel, les données sont regroupées par blocs de \(N_e\) échantillons, et pour chacun de ces blocs les opérations suivantes sont effectuées :

  • Fenêtrage et recouvrement (optionnel) : Afin de lisser les traitements d'un blocs à l'autre, une fenêtre d'apodisation peut être appliquée (par défaut, une fenêtre de Hann avec un recouvrement de 50 %, de manière à avoir une reconstruction parfaite).
  • Zéro-padding : De manière à avoir pouvoir calculer efficacement les FFT, des zéros sont ajoutés afin d'avoir des blocs dont la dimension est une puissance de 2. Après zéro-padding, la dimension des blocs vaut \(N=2^k\geq N_e\).
  • Transformée de Fourier : via une FFT.
  • Traitement dans le domaine fréquentiel : à faire par l'utilisateur (callback passée en paramètre, voir ci-dessous).
  • Transformée de Fourier inverse : via une FFT inverse.
  • Recomposition des blocs temporels : par OLA (OverLap-and-Add).

Note
Pour le problème plus spécifique du calcul efficace d'un filtre RIF (à partir de la FFT), utilisez plutôt filtre_rif_fft(), qui est est basée sur cette fonction, et qui plus simple à utiliser.

Exemple : Filtrage passe-bas

Dans cet exemple, on filtre passe-bas un signal en mettant tout simplement à zéro la moitié des composantes fréquentielles. 

  soit n = 8192;
  // signal utile à f = 0.04 * fe Hz, et parasite à f=0.400 * fe Hz
  soit x = (sigsin(0.004, n) + sigsin(0.4, n)).as<cfloat>();


  FiltreFFTConfig config;
  // Cette callback sera appelée à chaque itération de l'OLA
  config.lien non trouvé : [structtsd_1_1fourier_1_1_filtre_f_f_t_config_1aaafe883d1d85de5c5d73b84151377740]traitement_freq = [&](Veccf &X)
  {
    assertion(X.rows() == 512);
    X.segment(128, 256).setZero();
  };
  config.lien non trouvé : [structtsd_1_1fourier_1_1_filtre_f_f_t_config_1a60a2f094be904de71dceaa73e55abe4a]dim_blocs_temporel   = 512;  // Par bloc de 512 échantillons
  config.lien non trouvé : [structtsd_1_1fourier_1_1_filtre_f_f_t_config_1a1d606b7442ae048364b6f3ddee03163a]nb_zeros_min         = 0;    // Zéro-padding non nécessaire
  config.lien non trouvé : [structtsd_1_1fourier_1_1_filtre_f_f_t_config_1abac3e46621762009cade415dbdbef694]avec_fenetrage       = oui;  // Fenêtre de Hann et recouvrement de 50 %

  soit [ola, N] = filtre_fft(config);
  soit y = real(ola->step(x));

Voir aussi

filtre_rif_fft(), filtre_rfft(), ola_complexité(), ola_complexité_optimise()