détecteur_création

Détecteur par corrélation.

Espace de nom : tsd::fourier

Prototype

sptr<Detecteur> détecteur_création(const DetecteurConfig &config=DetecteurConfig())

Paramètres

config

Structure de configuration

Retourne

Filtre cfloat \(\to\) float, qui prend en entrée des échantillons, et sort, au fil de l'eau, la corrélation normalisée avec le motif.

Description

Cette fonction calcule, au fil de l'eau, la corrélation normalisée entre un signal \((x_k)\) reçu en continu et un motif fixe \((h_k)\) de dimension \(M\) : \[ c_n = \frac{\left|\displaystyle{\sum_{k=0}^{M-1} x_{n+k} \cdot h_{k}^\star}\right|}{\displaystyle{ \sqrt{\left(\sum_{k=0}^{M-1}\left|x_{n+k}\right|^2\right) \left(\sum_{k=0}^{M-1}\left|h_k\right|^2\right)}}} \]

Les \(c_n\) sont donc compris entre 0 et 1, et seront égaux à 1 uniquement si le signal est exactement égal au motif (à un facteur d'échelle constant près) sur l'intervalle \([n\dots n + M[\).

Le calcul pouvant être fait soit grâce à un filtre RIF (avec une complexité de l'ordre de \(M\) opérations / échantillon), soit de manière efficace dans le domaine fréquentiel via la technique Overlap-And-Add (bloc filtre_fft()), la complexité étant alors de l'ordre de \(\log_2(M)\) opérations par échantillon (si \(M\) est une puissance de 2).

Ensuite, les pics isolés correspondant à des positions possibles de motif sont détectés. Les deux critères suivants sont vérifiés~:

Score \(c_n\) supérieur à un seuil paramétrable,
Absence de pic de score supérieur dans un voisinage de \(\pm\) la moitié de la durée du motif de synchronisation.

Pour chaque position possible, les paramètres suivants sont alors estimés : Gain complexe du signal (rapport complexe entre le signal reçu et le motif théorique attendu) : \[ g \sim \frac{\displaystyle{\sum_{k=0}^{M-1} x_{n+k} \cdot h_k^\star}}{\displaystyle{\sum_{k=0}^{M-1} |h_k|^2}} \] De cette valeur complexe, on en déduit le gain en amplitude et le déphasage : \[ A = \left|g\right|,\quad \phi = \arg g \]Ecart-type du bruit et SNR : Pour estimer le niveau de bruit, on note simplement que \(x_n - g^\star h_n \sim x_n - g h_n = b_n\), ainsi il suffit de mesurer l'énergie du signal \(x_n - g h_n\) pour avoir le niveau du bruit : \[ \epsilon_b \sim \mathbb{E}\left[\left|x_n - g h_n\right|^2\right] \] Cependant, le signal reçu sera en général affecté d'un retard non entier qui, si il ne posera pas de problème pour l'estimation de gain (puisque le signal est suréchantillonné), pourrait conduire sur-estimer le bruit. C'est pourquoi avant estimation de celui-ci, le signal est décalé d'un pas fractionnaire afin de minimiser l'erreur.

Pour chaque motif détecté, une callback utilisateur est appelée, avec l'ensemble des paramètres estimés ainsi que le score de corrélation normalisé.

Schéma-bloc

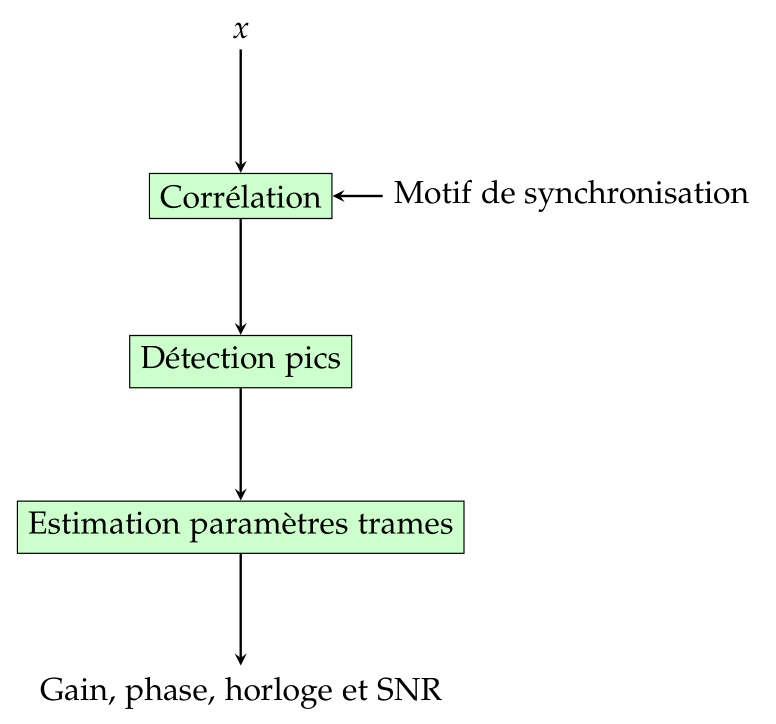
Exemple

  soit M = 512;  // Dimension du motif
  soit N = 16*M; // Dimension du signal

  // Motif de synchronisation
  soit motif = sigchirp(0.001, 0.2, M, 'q');

  // Signal = bruit
  soit x = (0.1 * randn(N)).as<cfloat>();

  // + motif à détecter au milieu
  x.segment(900, M) = motif;

  soit pos_detection = 0;

  DetecteurConfig config;
  config.motif  = motif;
  config.Ne     = M;
  config.lien non trouvé : [structtsd_1_1fourier_1_1_detecteur_config_1ac6388199c133574b9aa9061ced1f407f]gere_detection = [&](const Detection &det)
  {
    msg("Detection : {}.", det);
    pos_detection = det.position;
  };
  soit det = détecteur_création(config);
  soit y = det->step(x);

  Figures f;
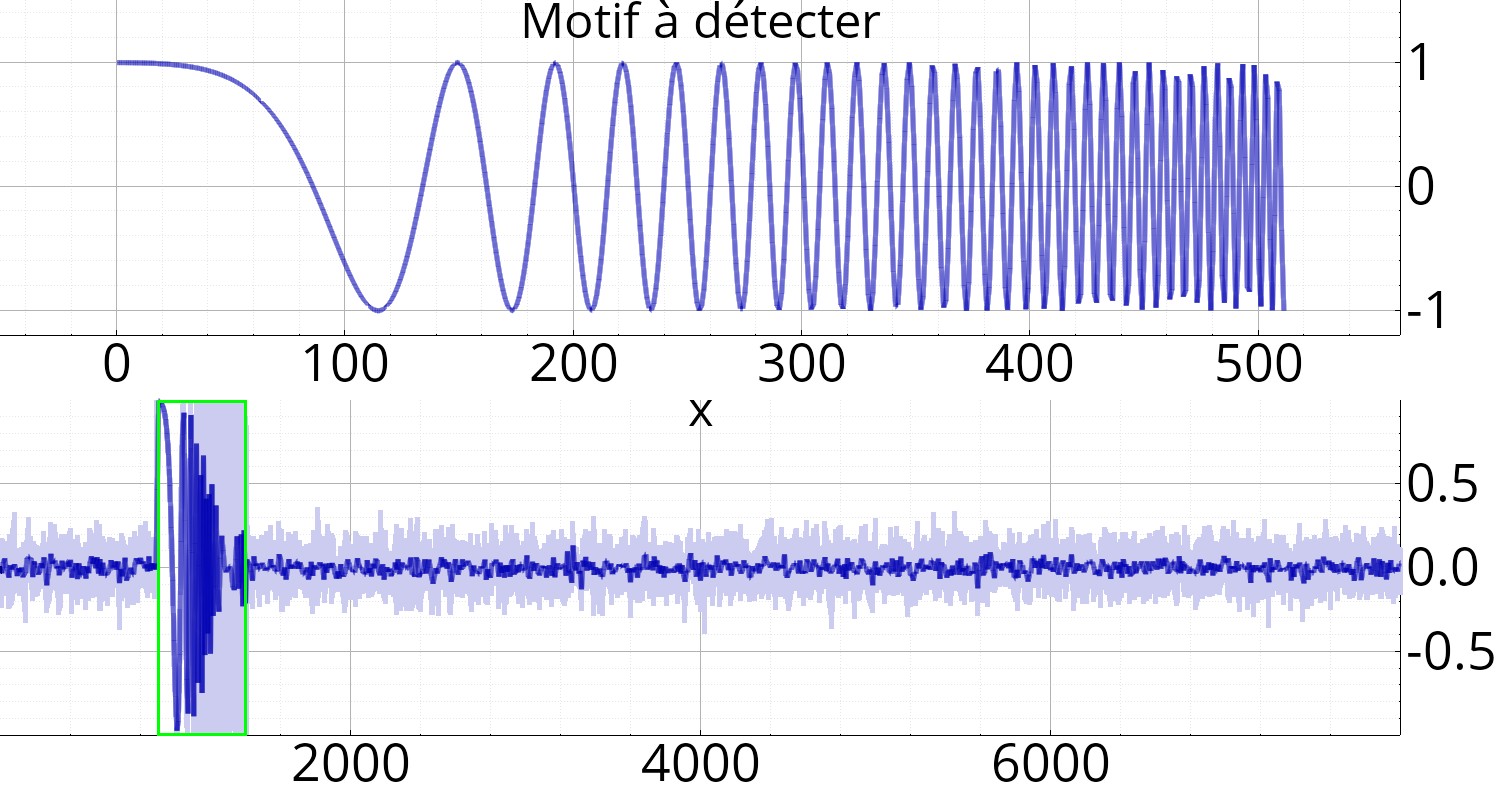
  f.subplot().plot(real(motif), "", "Motif à détecter");
  f.subplot().plot(real(x), "", "x");
  f.gcf().def_rdi({0, -1, 8000, 2});

  f.gcf().canva().set_couleur(tsd::vue::Couleur::Vert);
  f.gcf().canva().set_epaisseur(3);
  f.gcf().canva().set_remplissage(non);
  f.gcf().canva().rectangle(pos_detection, 1, pos_detection + M - 1, -1);