xcorr
Corrélation (non biaisée) entre deux vecteurs complexes.
Espace de nom : tsd::fourier
Prototype
tuple<Vecf, Veccf> xcorr(const Veccf &x, const Veccf &y=Veccf(), entier m=-1)
Paramètres
| x | Premier vecteur |
| y | Deuxième vecteur (éventuellement égal au premier pour avoir l'auto-corrélation) |
| m | Nombre de délais à examiner (si négatif, alors fait comme si \(m=N\)). |
Retourne
Un tuple de deux vecteurs de dimension \(2m-1\) : délais \(\tau_k\) et corrélation \(c(\tau_k)\).
Description
Calcule la corrélation entre deux signaux complexes (calcul efficace via des FFT), soit pour un délais négatif ( \(\tau=-(m-1)\dots -1\)) :
Les délais étant échantillonnés de manière régulière entre \(-(m-1)\) et \(m-1\) :
- Note
- Les signaux sont complétés en interne avec des zéros pour pouvoir effectuer efficacement la corrélation dans le domaine fréquentiel.
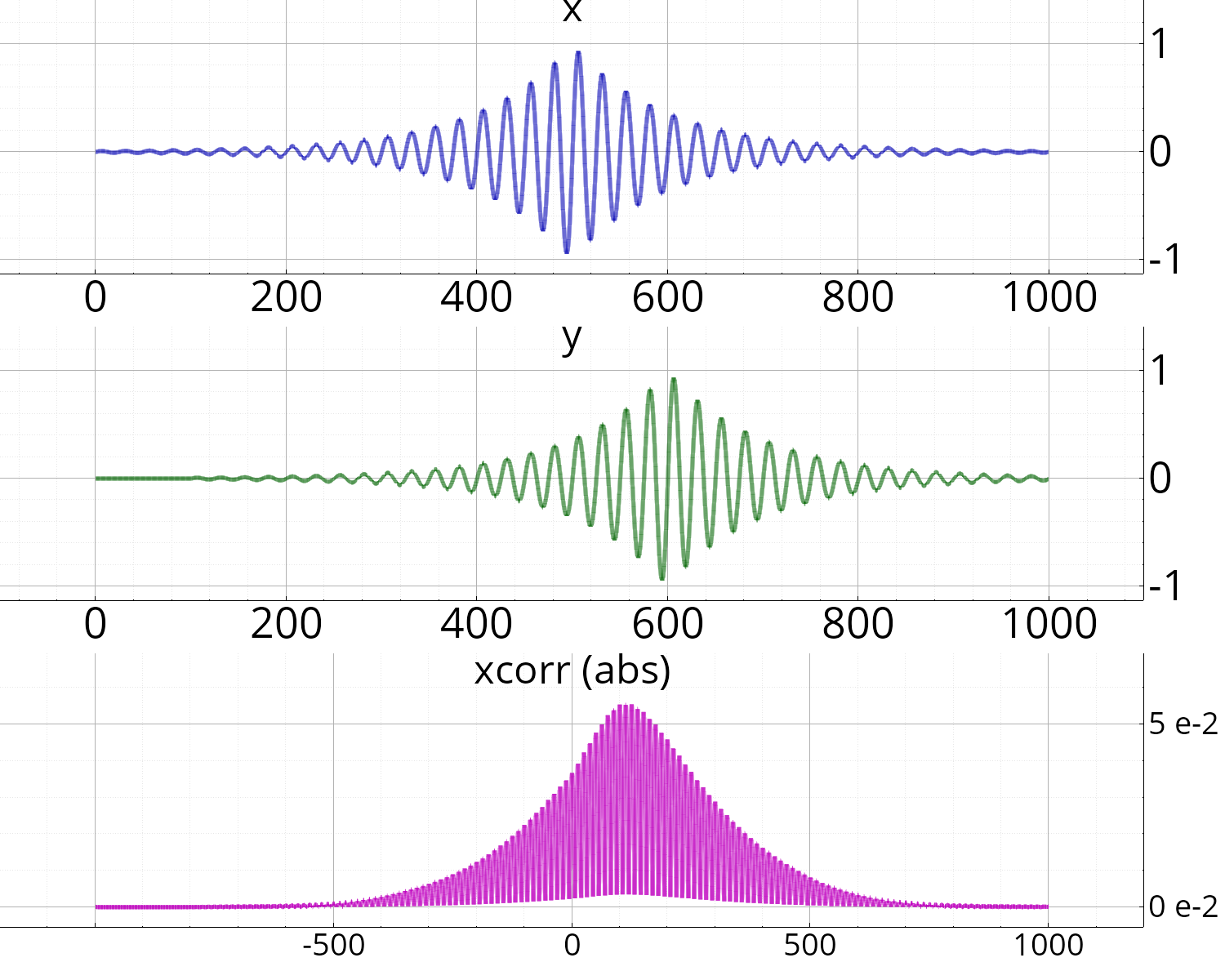
Exemple
soit x = sigsin(0.04, 1000) * exp(-abs(linspace(-5,5,1000))),
y = délais(x, 100);
soit [lags, c] = xcorr(x, y);
Figures f;
f.subplot().plot(x, "b-" , "x" );
f.subplot().plot(y, "g-" , "y" );
f.subplot().plot(lags, abs(c), "m-" , "xcorr (abs)" );