psd_sousesp

Calcul d'un spectre par la méthode des sous-espaces.

Espace de nom : tsd::fourier

Prototype

tuple<Vecf, Vecf> psd_sousesp(const Veccf &x, entier Ns, entier Nf=1024, entier m=0)

Paramètres

x	Signal à analyser
Ns	Nombre d'exponentielles pures attendues
Nf	Résolution fréquentielle (en nombre de points)
m	Dimension de la matrice d'auto-corrélation (si non précisé = dimension du signal)

Retourne

Un tuple de deux éléments : vecteur de fréquences (normalisées, entre -0.5 et 0.5), et le spectre.

Description

Cette technique d'estimation spectrale est une méthode paramétrique, qui suppose que le signal est constitué de la somme d'un nombre fini et connu d'exponentielles pures.

La formule utilisée ici est celle de l'algorithme MUSIC (MUltiple SIgnal Classification).

Note

Cette fonction est une spécialisation de la méthode des sous-espaces pour la détection d'exponentielles pures. Cependant, la méthode des sous-espaces elle-même est bien plus générale, et peut permettre de détecter d'autres types de signaux (voir la fonction tsd::stats::subspace_spectrum()).

Avertissement

Cette technique implique la décomposition en valeurs propres d'une matrice \(m\times m\) (la matrice d'auto-corrélation du signal), soit de l'ordre de \(m^3\) opérations. Par conséquent, si la dimension du signal est importante, il est conseillé de choisir un \(m\) plus petit.

Exemple : détection de 3 exponentielles pures

  soit nfreqs = 3, n = 256;

  // Signal constitué de bruit blanc...
  Veccf x = randn(n);

  // ... et de 3 fréquences pures
  pour(auto f: {0.113423, 0.212213, 0.323432})
    x += sigexp(f, n);

  // Algorithme MUSIC : 3 exponentielles, matrice d'auto-corrél 32x32
  soit [fr, Smu] = psd_sousesp(x, nfreqs, 1024, 32);

  Figures f;
  f.subplot().plot(x, "", "x");
  f.subplot().plot_psd(x);
  f.gcf().titres("PSD (corrélogramme)", "Fréquence");
  f.subplot().plot(fr, Smu);
  f.gcf().titres("PSD (MUSIC)", "Fréquence");

Spectre PSD vs MUSIC :

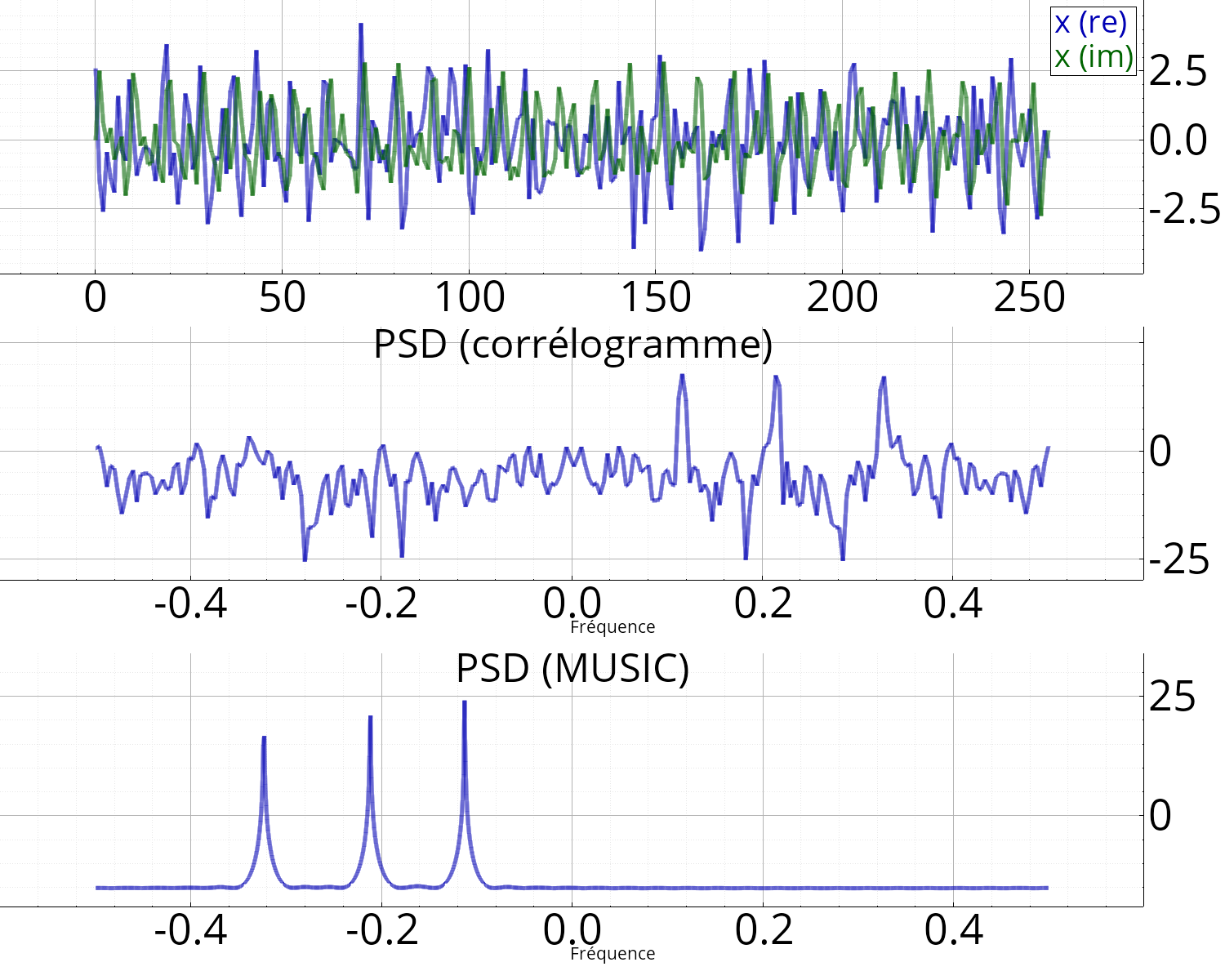
Notez comme le spectre MUSIC est plus propre ; il ne faut cependant pas oublier que cette technique suppose connu le nombre de signaux (ici 3).

Note

Pour la détection de sinusoïdes pures (signaux réels), il faudra choisir \(N_s\) comme étant deux fois le nombre de signaux à détecter (en effet, un cosinus ou sinus peut se représenter comme la somme de deux exponentielles complexes).

Voir aussi

tsd::stats::subspace_spectrum()